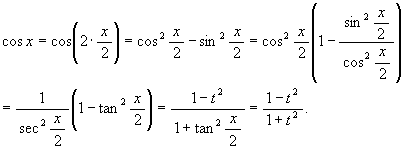
F を有理函数として ∫F(cos x, sin x) dx を考える。 媒介変数として t = tan (x/2) と置くと
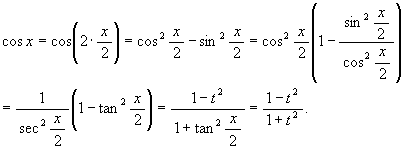
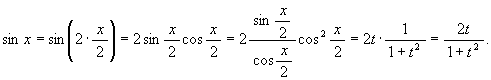
ある site でこういう証明よりも cos x = (cos2(x/2) - sin2(x/2))/(cos2(x/2) + sin2(x/2)) の分子分母を cos2(x/2) で割るという証明の方が好きだという意見を頂いた (sin の方も同様)。 確かにそっちの方がいいので一言書いておく。
従って
![]()
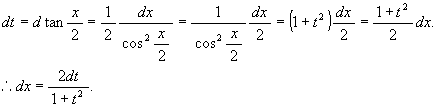
というわけで結局
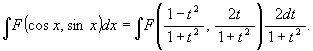
注:
F(cos x, sin x) が, tan x, cos 2x, sin 2x, sin2 x, cos2 x, sin x cos x 等のように全ての周期が π である場合には, 上記のかわりに t = tan x で積分できる。
例は長くなるのでこちらへ。
t = tan(θ/2) と置くわけ。
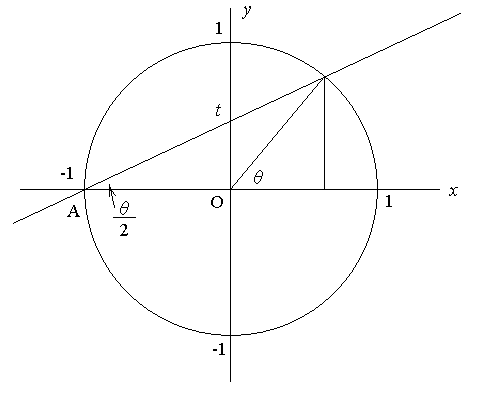
図のように単位円周上の A(-1, 0) を通る直線で, x 軸の正の部分となす角を θ/2 と置くようにする。 このときこの直線の y 切片は t となるので,
その方程式は y = t(x + 1) となる。
単位円周の方程式 x2 + y2 = 1 と連立させて, 最初の点
A とは異なる交点の座標を求めよう。
すると x2 - 1 + t2(x + 1)2 = 0.
(x + 1)(x - 1 + t2(x + 1)) = 0
ここで x ≠ -1 なので, 後ろの因子から (t2 + 1)x + (t2 - 1) = 0.
従って x = (1 - t2)/(1 + t2) = cosθ,
y = t((1 - t2)/(1 + t2) + 1) = 2t/(1 + t2)) =
sinθ.
この置き方から, この置換で (-1, 0) が除外されているわけも分かる。
Friday, 4th December, 2009.