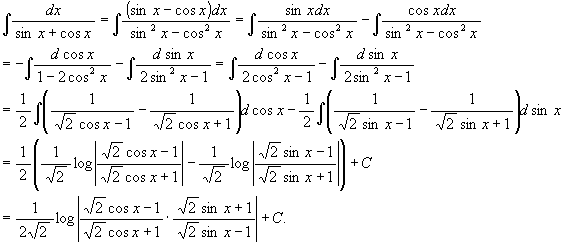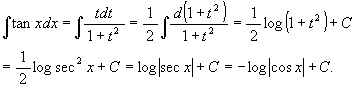
三角函数の積分の例

以下, 積分定数として C を用いる場合にはいちいち断らない。

(1) ∫tan x dx

[解 1] t = tan x と置くと, dt = sec²x dx = (1 + tan²x)dx = (1 + t²)dx.

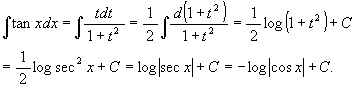
[解 2] (こっちの方が普通である)

(2) ∫sec x dx.

[解 1] (こっちが普通である)

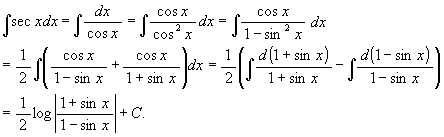
[解 2] t = tan(x/2) と置く。

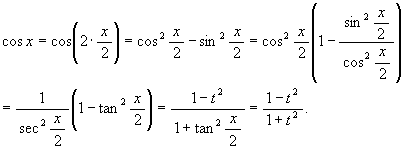
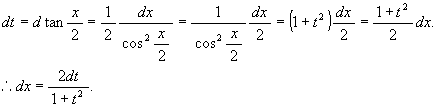
より

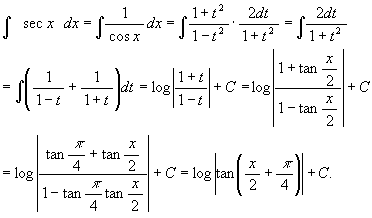
これで一応終りだが, 答えが一致している感じがしないので, 一致していることを確かめてみよう。

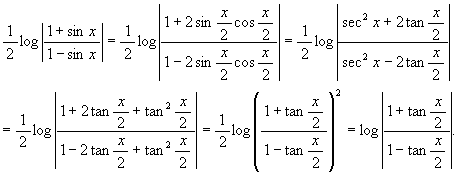
(3) ∫sin³x dx

[解 1] 三倍角の公式より sin 3x = 3sin x - 4 sin³x であるから,

故に

[解 2] (see 漸化式)

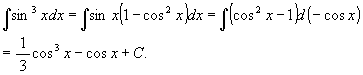
またまた結果が違うような気がするが, 三倍角の公式から同じであることが分かる。

(4) (詳細略)

(5) (詳細略)

(6) (詳細略)

(7)

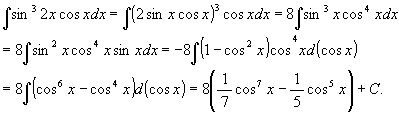
(8)

[解 1] t = tan(x/2) と置いて

[解 2]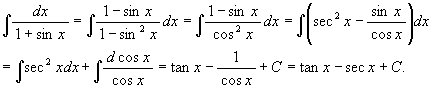

因みに

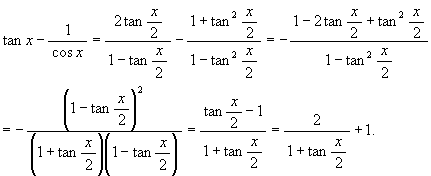
で, 定数 1 は積分定数 C に吸収できるので問題にならない。

(9)

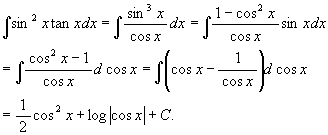
因みにこれを t = tan x と置いてやってみたが, 上手く行かなかった。

(10)

[解 1] t = tan x と置くと

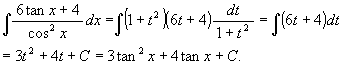
[解 2]

[解 3]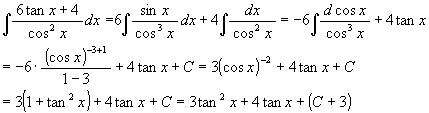 

(11)

[解 1] t = tan(x/2) と置くと

[解 2] 途中で (5) を無断で用いる。

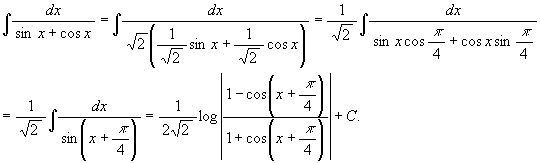
因みに (途中で半角公式を用いている)

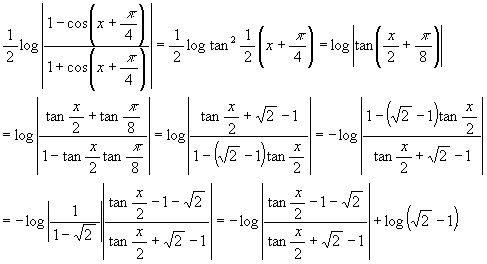
[解 3]

戻る