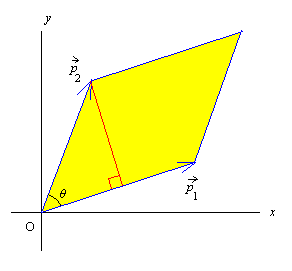
D を P で変換するとP(se1 + te2) = sp1 + tp2,
0 ≦ s ≦ 1, 0 ≦ t ≦ 1
であるから, D の面積 A は
A = |p1||p2| sin ∠(p1, p2)
= |p1||p2|√sin2∠(p1, p2)
= |p1||p2|√(1 - cos2∠(p1, p2))
= √(|p1|2|p2|2 - (|p1||p2|cos ∠(p1, p2))2)
= √(|p1|2|p2|2 - (p1・p2)2).
以前に 「積分 1」 の 「面積」 のところで述べたように, 面積とは x 軸方向に 1, y 軸方向に 1 の正方形が幾つ入るかということが基本になっているのだった。 今, 或る図形の面積が S だったとす同一直線上に映されるということから が張る正方形, つまり D: se1 + te2, の表す領域の面積が S 個分であるということを意味していると考えて良い。
今この図形を P = (pi) によって変換したとしよう。 この時, 面積は何倍になるであろうか ? その倍率を求めれば良い。
D を P で変換すると
P(se1 + te2) =
sp1 + tp2,
0 ≦ s ≦ 1, 0 ≦ t ≦
1
であるから, D の面積 A は
A = |p1||p2| sin
∠(p1, p2)
= |p1||p2|√sin2∠(p1, p2)
=
|p1||p2|√(1 - cos2∠(p1, p2))
= √(|p1|2|p2|2
- (|p1||p2|cos ∠(p1, p2))2)
= √(|p1|2|p2|2
- (p1・p2)2).
さて一方 pk = p1ke1
+ p2ke2 と書けるから
|p1|2|p2|2
- (p1・p2)2
= (p112 + p212)(p122
+ p222) - (p11p12 + p21p22)2.
= p112p122 + p112p222
+ p212p122 + p212p222
- (p112p122 + 2p11p12p21p22
+ p212p222)
= p112p222 - 2p11p12p21p22
+ p212p122
= (p11p22 - p21p12)2
= det(P)2.
従って A = √(det(P)2) = |det(P)| (外側の縦棒は絶対値).よって次のことが分かった。
定理
行列 P によって面積 S の図形を変換すると, その面積は |det(P)| 倍になる。
このことから直ちに正則でない行列 P で図形を変換すると面積は 0 に成ってしまうことが分かる。 それは P(ei) が同一直線上に移されるということから (一本の直線上に潰されてしまうので) 明らかであろう。