を考えよう。前の page の終わり頃に出て来た二種類の行列 A = (a11 a12), B =
を考えよう。
先ず A = (a11 a12) と同じ style (つまり行が一つ, 列が二つの行列) の行列全体も行列の一種であるから, 和と差, 実数倍が定義されて, 「一次変換と行列の加・減法, 実数倍」 の最後に書いた八つの性質を満足する。 従ってこのようなものは (平面の) vectors と同じ (唯真ん中に "," がないだけ) である。 この style の行列は行の数が 1, 列の数が 2 なので 1×2 型の行列と呼ばれるが, vector としての性質も持っているので, これを vector と考えて
行ベクトル row vector
という。 行列の積の基本は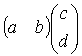 
= ac + bd
であるので, 行ベクトルと積が考えられるのは, (今のところ) これと
(x y)
= (ax + cy bx + dy)
と 
だけである (もっと様々な行列 style の行列と
積が取れることがあとで分かる)。
次に B =
と同じ style についても同様のことがいわれる。 この
style の行列は 2×1 型の行列, 又は列ベクトル column vector という。 列ベクトルと積がとれるのは
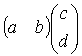= ac + bd と
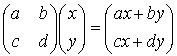である。
行ベクトルと列ベクトルの席をとっている式 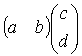= ac + bd
は良くみると双対ベクトルを考えているのと同等であることが分かる。 即ち vector a
= (a11 a12) に対し
a* =
とすれば行ベクトル x に対し, 行列の積として
x・a = xa*
となっている。 即ち行列の積は内積の拡張である。
「一次変換を表す行列」 で扱った行列は 2×2 型の行列又は二次の正方行列 square matrices と呼ばれる。
但し, aj = (aj1 aj2), aj
= 
と置くとき, この各々を, 行列 (ajk)
の行分解, 列分解と呼び, vectors aj, aj
を各々行成分 (ベクトル), 列成分 (ベクトル) という。 この書き方に拠れば, 二次正方行列同士の積は
(ajk)(bjk) = (ajd)(bdk)
= 
と書ける。 これを又 (ajk)(bjk) = (ajd)(bdk)
= (aj)(bk) = (ajbk)
と書くこともある。 更に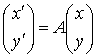 
という式は 列ベクトル
x, y を用いて y = Ax とも書かれる
(こう書くと一次函数との類似が一層はっきりする)。
物理の方では行ベクトルを <a|, 列ベクトルを |b> のように書いて, 各々ブラベクトル bra-vector, ケットベクトル ket-vector という。 これは二つあわせて <a|b> が内積 (bracket) になるという洒落なのである。