
二つ以上の不等式が組み合わされて出来ている一組の不等式を連立不等式 simultaneous inequalities, simultaneous system of inequalities という。 これらの不等式を同時に満たす x の値の範囲を連立不等式の解といい, 解を求めることをその連立不等式を解くという。
例:
(1) 
(2) -5x < 3(x - 8) < x - 12.
解:
(1) 先ず (a) を解くと 5x < 10 より x < 2 … (c).
次に (b) を解くと -x ≧ -1 より x ≦ 1 … (d).
これらを同時に数直線上に表して, 共通な部分を求めればいいから
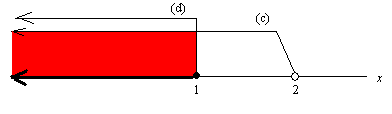
となって x ≦ 1.
(2) これは -5x < 3(x - 8) と 3(x - 8) < x - 12 の二つに分解される。 先ず前半は
-5x < 3x - 24 より -8x < -24. 即ち x > 3 … (a).
後半から 3x - 24 < x - 12 より 2x < 12 即ち x < 6 … (b).
これらを同時に数直線上に表して共通な部分を求めれば良いから

となって 3 < x < 6.
注: (2) のように A < B < C 型の連立不等式は A < B と B < C と分けて解けばよい。
連立方程式の場合には A = B = C 型のものは A = B と B = C に分ける他に, A = B, A = C という分け方, A = C, B = C という分け方があり, どの分け方でも正しい答えを出すことが出来るが, 連立不等式の場合にはそうはいかない。
例えば (2) で -5x < x - 12 と 3(x - 8) < x - 12 と分けたとすると, 前半は x > 2, 後半は x < 6 だから 2 < x < 6 となるが, 例えば x = 5/2 を考えると
-5x = -25/2, 3(x - 8) = -33/2, x - 12 = -19/2 となって, 元の -5x < 3(x - 8) < x - 12 を満たさない。
次へ
一次不等式の目次へ