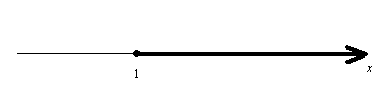
変数 x が出て来る不等式が与えられていて, それを成り立たせるような数 (の範囲) をその不等式の解 solution という。 又その不等式の解を (全て) 求めることをその不等式を解く solve という。
例: x は整数であるとして -3 < x ≦ 4 を解くと, x = -2, -1, 0, 1, 2, 3, 4.
普通の問題では x は整数とは限らないので, x > a とか, x < b とか, x ≧ c とか, x ≦ d とかいう形で求めることになる。 これらの範囲は次のように数直線で表される。
x ≧ 1 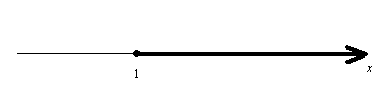
x > 1 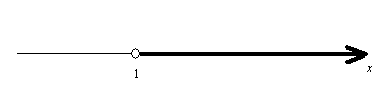
x ≦ 2 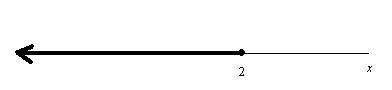
x < 2 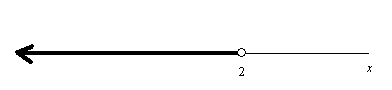
1 ≦ x < 2
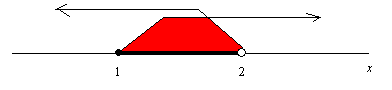
見て分かると思うが, 習慣として, ○ はその数が解に含まれていないことを示し, ● はその数が解に含まれることを示している。