解答

[2] の解答。

(1) とにかく, 面積の問題を見たらグラフもしくは増減表を書かねばならない。 というのはグラフの上下関係が重要だからである。

y' = 3x² - 2x - 1 = (3x + 1)(x - 1) --- 襷掛 (たすきがけ)。 又, 積分区間が [-1, 1] であることを考慮して

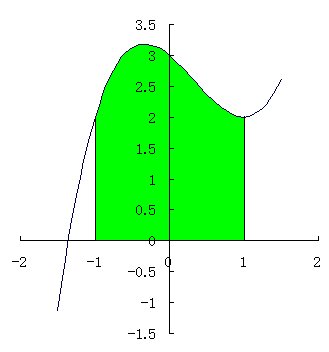
という増減表を得る。 一番低い所でも y = 2 だから, すべて x 軸の 「上方」 にある。 念のためにグラフを描くと

従って求める面積は

∫_-1¹(x³ - x² - x + 3) dx = [x⁴/4 - x³/3 - x²/2 + 3x]_-1¹
= (1/4 - 1/3 - 1/2 + 3) - (1/4 + 1/3 - 1/2 - 3)
= 1/4 - 1/3 - 1/2 + 3 - 1/4 - 1/3 + 1/2 + 3
= 2(-1/3 + 3) = 2×8/3 = 16/3.

ここで注目して欲しいのは x³ と x の定積分の部分は消えてしまって, x² と 3 の定積分の部分だけ生き残っていることである。 これは補遺のところで細かく説明する。

又, 面積なので - の値が出てきたら先ず間違いである。

(2) y = -(x² - 6x + 5) = -(x - 1)(x - 5)

からグラフの概形はすぐわかる。

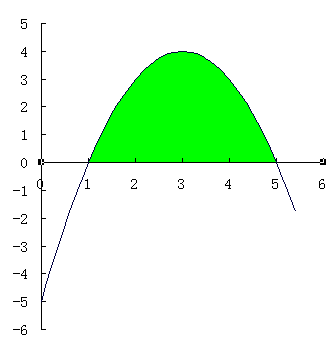
よって求める面積は

∫₁⁵(-x² + 6x - 5)dx = [-x³/3 + 3x² - 5x]₁⁵
= (-125/3 + 75 - 25) - (-1/3 + 3 - 5)
= -125/3 + 50 + 1/3 + 2
= -124/3 + 52 = 32/3.

(3) y = (x + 1)(x² - 6x + 8) = (x + 1)(x - 2)(x - 4) --- 因数定理。

これから, + , - と x 切片 (x 軸との交わり) を考えると次のようなグラフが得られる。

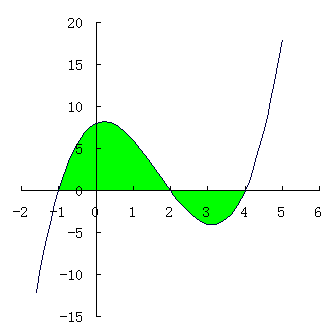
グラフが x 軸よりも下にある部分の面積であるが, 面積のときに説明したように, もともと, 縦の長さ f(x)×微小な幅 dx を a から b 迄足していったものが定積分 だったのだから, x 軸より下にある場合は f(x) < 0 なので, 縦の長さとして -f(x) を採用しなければならない。

従って求める面積は

∫_-1²(x³ - 5x² + 2x + 8) dx - ∫₂⁴(x³ - 5x² + 2x + 8) dx
= [x⁴/4 - 5x³/3 + x² + 8x]_-1² - [x ⁴/4 - 5x³/3 + x² + 8x]₂⁴
= (4 - 40/3 + 4 + 16) - (1/4 + 5/3 + 1 - 8) - (64 - 320/3 + 16 + 32) + (4 - 40/3 + 4 + 16)
= 2×(24 - 40/3) - 1/4 - 5/3 + 7 - 112 + 320/3
= 48 - 80/3 - 5/3 + 320/3 -1/4 - 105
= 235/3 - 1/4 - 57 = (940 - 3 - 684)/12 = 253/12.

注: 絶対値を a ≧ 0 に対して |a| = a, a < 0 に対して, |a| = -a と決めると, これは, x = a から x = b までで y = f(x) のグラフと x 軸とで囲まれる部分の面積が ∫_a^b|f(x)|dx と表されることを示している。

(4) 交点を求める為に x² - 2x = 6x - x² と置くと, 2x² - 8x = 2x(x - 4) = 0 なので, x = 0, 4.

放物線なので二次の係数を見れば凹凸が分かるので下図のようなグラフを得る。

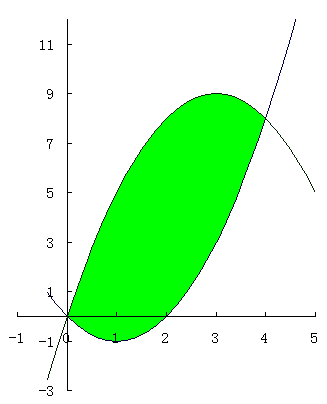
(3) でも説明したが, 縦の長さ×微小な幅 dx の和が, 定積分だから, 面積は上のグラフの式 - 下のグラフの式 の積分をすればよい。

従って求める面積は

∫₀⁴((6x - x²) - (x² - 2x))dx = ∫₀⁴(-2x² + 8x) dx
= [-2x³/3 + 4x²]₀⁴ = (-(64×2)/3 + 64) - 0 = (-64×2 + 64×3)/3
= 64×(-2 + 3)/3 = 64/3.

上記の事を纏めると, 区間 [a, b] で, y = f(x) と y = g(x) のグラフが囲む部分の面積は

∫_a^b|f(x) - g(x)| dx

ということになる。