であった。「微分 2」 の 「指数函数と対数函数の微分」 に於いて一応定義だけはしたが, かなりいい加減だったのでここで収束などをちゃんとやる。
定義は
であった。
先ず an = (1 + 1/n)n と置いて, これが収束することを言おう。
二項定理によって,
an = 1 + nC1・1/n + nC2(1/n)2
+ nC3(1/n)3 + … + nCn(1/n)n
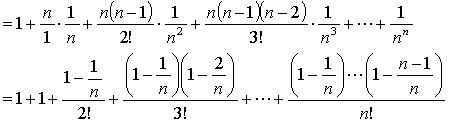
ここで n から n + 1 になると, 例えば (1 - 1/n)/(2!) < (1 - 1/(n+1)/(2!) のように, 各項は増大し, しかも項数も増加するのだから, 数列 {an} は (狭義) 単調増加である。 しかも 0 < 1 - k/n < 1 であるから
an < 1/(0!) + 1/(1!) + 1/(2!) + 1/(3!) + … + 1/(n!)
< 1 + 1 + 1/2 + 1/22 + 1/23 + … + 1/2n-1
= 2 + (1/2)(1 - (1/2)n-1)/(1 - 1/2) = 2 + 1 - (1/2)n-1 = 3
- (1/2)n-1 < 3.
というわけで単調増大且つ上に有界だから収束する。
この定義が 「古典的」 なのは, 収束が極めて遅い上に, (1 ± 0)±0 というのは computer 上では誤差が沢山出ることが分かっているので, 実際には Taylor-Maclaurin 級数を用いて e = Σn = 0∞ 1/n! として計算するのが普通だからである。
ところで 「指数函数と対数函数の微分」 で必要だったのは, 本当は
ではなくて
なのだった (本当は t → -∞ の方も必要なのだが, それは下の例の (5) で)。 そこで, t が整数だけではなくて, 実数の場合にもこれが e
になるということを証明しておくことにしよう。
先ず t → ∞ であるから, t > 0 として良い。 このとき, 適当な自然数 n が存在して n ≦ t < n + 1 と出来る。 このとき明らかに
1/(n + 1) < 1/t ≦ 1/n
1 + 1/(n + 1) < 1 + 1/t ≦ 1 + 1/n
(1 + 1/(n + 1))n < (1 + 1/t)n < (1 + 1/t)t ≦ (1
+ 1/n)t < (1 + 1/n)n+1
即ち
(1 + 1/(n + 1))n < (1 + 1/t)t < (1 + 1/n)n+1.
書き直すと
(1 + 1/(n + 1))n+1/(1 + 1/(n + 1)) < (1 + 1/t)t < (1 + 1/n)n(1 + 1/n).
従って t ≧ n だから n → ∞ とすると e ≦
≦
e となるので, 結局
=
e であることが分かる。
例: a, b は定数で ab ≠ 0 とする。
(1) limn→∞ (1 + 1/n)-n.
(2) limx→+0 (1 + x)1/x.
(3) limx→-∞ (1 - 1/x)x.
(4) limx→-0 (1 - x)-1/x.
(5) limx→-∞ (1 + 1/x)x.
(6) limx→-0 (1 + x)1/x.
(7) limx→0 (1 - x)1/x.
(8) limx→∞ (1 +a/x)bx.
(9) limx→∞ (1 + x)1/x.
解答:
(1) limn→∞ (1 + 1/n)-n = limn→∞ 1/(1 + 1/n)n
= 1/limn→∞ (1 + 1/n)n = 1/e.
(2) t = 1/x と置くと, x → +0 の時 t → +∞ なので
limx→+0 (1 + x)1/x = limt→+∞ (1 + 1/t)t
= e.
(3) t = -x と置けば, x → -∞ の時 t → +∞ なので
limx→-∞ (1 - 1/x)x = limt→+∞ (1 + 1/t)-t
= 1/e.
(4) t = -1/x と置くと, x → -0 の時 t → +∞ なので
limx→-0 (1 - x)-1/x = limt→+∞ (1 + 1/t)t
= e.
(5) t = -x と置けば, x → -∞ の時 t → +∞ なので
limx→-∞ (1 + 1/x)x = limt→+∞ (1 - 1/t)-t
= limt→+∞ ((t - 1)/t)-t
= limt→+∞ (t/(t - 1))t
= limt→+∞ ((t - 1 + 1)/(t - 1))t
= limt→+∞ (1 + 1/(t - 1))t
= limt→+∞ ((1 + 1/(t - 1))t-1・(1 + 1/(t - 1)))
= limt→+∞ (1 + 1/(t - 1))t-1・limt→+∞ (1 + 1/(t
- 1)) = e.
(6) t = 1/x と置けば x → -0 の時 t → -∞ なので (5) より
limx→-0 (1 + x)1/x = limt→-∞ (1 + 1/t)t
= e.
(7) x = -1/t と置くと x→±0 の時 t → ±∞ であるから
limx→0 (1 - x)1/x = limt→±∞ (1 + 1/t)-t
= 1/e.
(8) t = 1/(ax) と置くと, x → ∞ の時 t → (sign a)∞ (sign a とは a の符号のことで, a > 0 の時
+1, a < 0 の時 -1 である)
limx→∞ (1 +a/x)bx = limt→(sign a)∞ (1 + 1/t)abt
= (limt→(sign a)∞ (1 + 1/t)t)ab = eab.
(9) 「n 乗根の極限」 でやったように, limn→∞ n√n = 1 従って (1 + n)1/n = ((1 + n)1/(n+ 1))(n+1)/n = ((1 + n)1/(n+ 1))1 + 1/n → 11 = 1 (as n → ∞).
このやり方が粗雑で気になる人は, そこの証明と同じように n ≧ 1 ⇒ (1 + n)1/n > 1 であることに注目して, (1
+ n)1/n = 1 + αn と置いて αn > 0 であることから二項定理を用いて
n ≧ 2 の時
1 + n > (1 + αn)n > (n(n - 1)/2)αn2
+ １
だから 0 < αn < 2/(n - 1) → 0 (as n → ∞) から言えばよい。
ここで上記と同様に n ≦ x < n + 1 と出来ることを用いて上下から挟んでいけば, limx→∞ (1 + x)1/x = 1 であることが分かる。
練習: a, b は定数で ab ≠ 0 とする。
(1) limx→-0 (1 - x)1/x.
(2) limn→∞ (1 - 1/n)-n.
(3) limx→∞ (1 - 1/x)x.
(4) limx→0 (1 + ax)b/x.
(5) limx→∞ (1 + 2/x)3x.
(6) limx→0 (1 - x)2/x.
(7) limx→0 (1 - x/2)-1/x.
(8) limx→0 (1 + x)1/(2x).
(9) limx→-∞ (1 - 2/x)-x/2.
(10) limx→+0 (1 + 1/x)x.
略解:
(1) 1/e, (2) e, (3) 1/e, (4) eab, (5) e6, (6) 1/e2, (7) √e (= e1/2), (8) √e (= e1/2), (9) e, (10) 1 (例 (9) による).
ちょっとした公式の纏め: