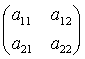 , B =
, B =
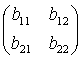 と表される。 ここで (x', y') = (f +
g)(x, y) と置くと、 成分表示によって
と表される。 ここで (x', y') = (f +
g)(x, y) と置くと、 成分表示によって二つの与えられた一次変換 f, g に対し, その和と差 f + g と f - g を考えよう。 今 h = f + g と置くと, この写像 h をどう定めたらよいかという問題である。 Vector x を任意にとり h(x) = (f + g)(x) を考えれば良いが, あたかも分配法則が成り立つかのように
(f + g)(x) = f(x) + g(x)
と定める (丁度双対ベクトルの様に)。 この時, この写像 h = f + g は一次変換である。 実際,
h(kx + my) = (f + g)(kx + my)
= f(kx + my) + g(kx + my)
= kf(x) +
mf(y) + kg(x) +
mg(y)
= k(f(x) + g(x)) + m(f(y) + g(y))
= k(f + g)(x) + m(f + g)(y)
= kh(x) + mh(y).
同様にして, (f - g)(x) = f(x) - g(x) と定めると f - g は一次変換となる。
次に実数倍 h = αf を考えよう。 これも同様に
(αf)(x) = α(f(x))
と定める。 これも一次変換である。 実際
h(kx + my) = (αf)(kx + my)
= α(f(kx + my))
= α(kf(x) +
mf(y))
= αkf(x) +
αmf(y)
= k(αf(x)) + m(αf(y))
= kh(x) + mh(y).
以上から一次変換全体の作る空間はベクトル空間のような性質をみたいしていることが直ぐ分かる。 但し 0 は零変換である。 f, g, h は一次変換, k, m は実数とすると,
[結合法則] (f + g) + h = f + (g + h),
[交換法則] f + g = g + f,
1・f = f,
k(f + g) = kf + kg,
k(mf) = (km)f,
(k + m)f = kf + mf,
f + 0 = f,
f + (-f) = 0.
今度は以上に述べたことを行列で表してみよう。 一次変換 f, g を成分表示して, 各々
x1' = a11x + a12y,
y1' = a21x + a22y;
x2' = b11x + b12y,
y2' = b21x + b22y
で表せば, f, g を表す行列 A, B は各々 A =
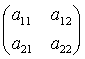 , B =
, B =
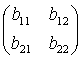 と表される。 ここで (x', y') = (f +
g)(x, y) と置くと、 成分表示によって
と表される。 ここで (x', y') = (f +
g)(x, y) と置くと、 成分表示によって
x' = x1' + x2' = (a11 + b11)x
+ (a12 + b12)y,
y' = y1' + y2' = (a21 + b21)x + (a22
+ b22)y.
故に f + g を表す行列を A + B と書くことにすると
A + B = 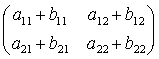
となる。 つまり (ajk) + (bjk) = (ajk + bjk) である。 これで行列 A = (ajk) と B = (bjk) の和を定める。
同様にして差の方も (ajk) - (bjk) = (ajk - bjk) で定める。
同様に (x', y') = (αf)(x, y) と置くと
x' = α(a11x + a12y) = αa11x +
αa12y,
y' = α(b21x + b22y) = αb21x + αb22y.
故に αf を表す行列を αA と書くと
αA = 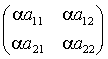
即ち α(ajk) = (αajk) によって実数倍を定める。
このようにすると, この page の上半分で述べたことに対応して 0 を零行列とするとき
(A + B) + C = A + (B + C),
A + B = B + A,
1・A = A,
k(A + B) = kA + kB,
k(mA) = (km)A,
(k + m)A = kA + mA,
A + 0 = A,
A + (-A) = 0
が成り立つことは直ぐに分かる。