右図に於て, 第二余弦公式より △ABC で1. ベクトルの成す角
二つの (自由) ベクトル a, b が共に 0 でないとき, 平行移動によって a = OA, b = OB となるようにする。 この時三点 O, A, B によって一つの部分空間が決定されるので, この平面上で平面でやったときと同様に a, b の成す角を定めることが出来る。 尚, そこで述べたように, 0 と a の成す角は定めない。
2. 内積の定義
平面でやったときと同様 a ≠ 0, b ≠ 0 のとき
a・b = |a||b|cos ∠(a, b)
で, 又 a = 0 又は b = 0 の場合には a・b = 0 と定める。
又 a ⊥ b ⇔ a・b = 0 と定義し, この時 a と b は垂直であるという。
3. 内積の性質
内積には次の性質がある。
[1] a・a = |a|2,
[2] a・b = b・a, [交換法則
commutative law]
[3] ∀k∈R((ka)・b = k(a・b)),
[4] (a + b)・c = a・c
+ b・c. [分配法則 associative law]
証明: a = 0 又は b = 0 の時は明らかだから, 以下では a ≠ 0, b ≠ 0 と仮定する。 {1] -- [3] は底空間の次元と無関係に平面の時の証明が通用する。 新たに証明が必要なのは, [4] の分配法則だけである。
三次元の場合の分配法則の証明には三段階を要する。
3.1 c ∈ Ra + Rb (即ち a, b, c が一次従属) の時
この時は平面の時の証明がそのまま通用する。
3.2 a⊥b & a⊥c の時
次の場合との区別を明らかにするために, 記号を替えて
x⊥y & x⊥z ⇒ (x + y)・z = y・z
を証明する。 x⊥z だから x・z = 0 なので, 上記 [4] と同等である。 y || z の時は 3.１ の場合であるから, それ以外の時を考えればよい。
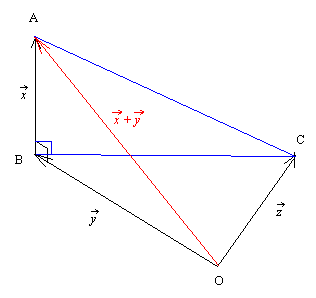
右図に於て, 第二余弦公式より △ABC で
|y - z|2 = |y|2 + |z|2 - 2y・z
同様に △OAC で
|(x + y) - z|2 = |x + y|2 + |z|2 - 2(x + y)・z.
従って △ABC で
|x + y|2 + |z|2 - 2(x + y)・z = (|y|2 + |z|2 - 2y・z) + |x|2.
△OAB で x⊥y より |x + y|2 = |x|2 + |y|2 が成立しているので結局
(x + y)・z = y・z.
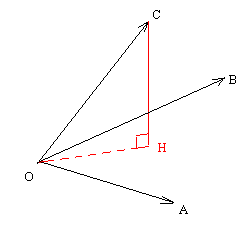
さて最後に一般の場合を証明する。 a, b, c は一次独立と仮定して良い。 A(a), B(b), C(c) と置くとき三垂線の定理によって C から平面 O∪A∪B への垂線の足 H を降ろすことが出来る。
この時 c = OH + HC であるが HC⊥a & HC⊥b, HC⊥OH なので, 直ぐ上の式で x = HC, y = OH, z = a + b と置く事によって
(a + b)・c = z・(OH
+ HC) = z・(x + y)
= (x + y)・z
= y・z … ここで上の式を使った
= OH・(a + b)
= (a + b)・OH = a・OH
+ b・OH … a, b, OH
は一次従属だから
= OH・a
+ OH・b = (OH + HC)・a
+ (OH + HC)・b … ここで上の式を逆に使った。
= c・a + c・b = a・c
+ b・c
となって証明された□
平面の時にも述べたが, 通常の教科書では座標と第二余弦公式とから, 成分で内積を表してから分配法則を代数的に証明することが普通である。 ここに書いた証明は私の original で, 他では見かけたことがない。
4. 成分表示
標準基底と成分の所で定義したように, |ex| = |ey| = |ez| = 1 であり, 三次元座標の定義により ex・ey = ey・ez = ez・ex = 0 が成立する。 従って 3 に述べた性質から a = (a1, a2, a3), b = (b1, b2, b3) とすると
a・b = (a1ex +
a2ey + a3ez)・(b1ex
+ b2ey + b3ez)
= a1b1|ex|2 + a2b2|ey|2
+ a3b3|ez|2
+ (a1b2 + a2b1)ex・ey
+ (a1b3 + a3b1)ez・ex
+ (a2b3 + a3b2)ey・ez
= a1b1 + a2b2 + a3b3
となる。