三次元の座標

ここで三次元空間の座標について述べておくことにする。 良く知られているように 平面 (= 二次元) の座標は右図に示されているような平面上の (向きの付けられた) 直交する二直線を座標軸として考えられている (実は直交していなくてもいいのだが直交していた方が色々便利なのである)。

今原点 O を通り, x 軸 y 軸に共に直交する直線 l を引く。 xy 平面上で時計回りの回転 (x 軸の正の向きから y 軸の正の向きの方向に向かう回転) を与えたとき, 所謂右螺子 (ねじ) が進んでいく方向, 即ち画面に対してこちら側 (あなたのいる方向) に正の方向を採った直線 l を z 軸と呼ぶ。

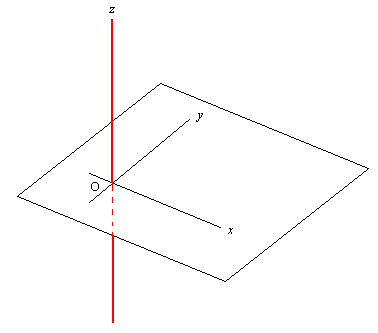
あとは平面と同様に考えて, 空間上の点 P の座標が定まるのである。

(上の図の立体は直方体である)

この図から三平方の定理を用いて

OP2 = OQ2 + PQ2 = x02 + y02 + z02

を得ることは明らかであろう。

次へ
三次元空間の vectors の目次へ