一次不等式と graph の関係を見てみよう。
y = f(x) = ax + b, a ≠ 0 として不等式 f(x) > 0 を考えてみる。
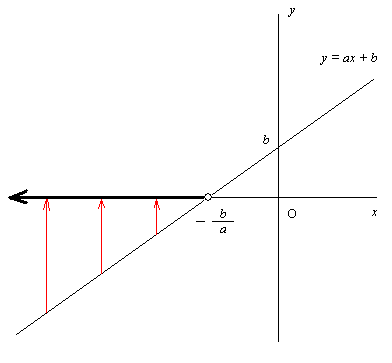
先ず普通に解くと ax + b > 0 より ax > -b. 従って x > -b/a である。
y = f(x) の graph を描くと, y = f(x) > 0 を解くことになるのだから, y > 0, 即ち, graph の (線の) x 軸より上の部分に出ている所を作っている点の x 座標の範囲を求めていることになるわけである。

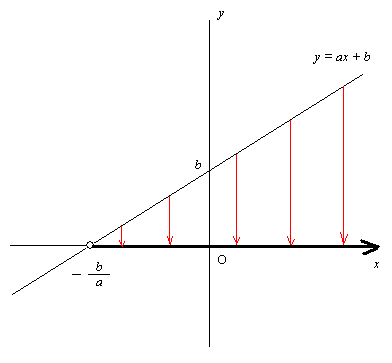
y = f(x) < 0 を解くことを考えると, これは同様にして y = f(x) の graph の x 軸より下に出ているところを作っている直線を構成している点の x 座標の範囲を求めていることになる。
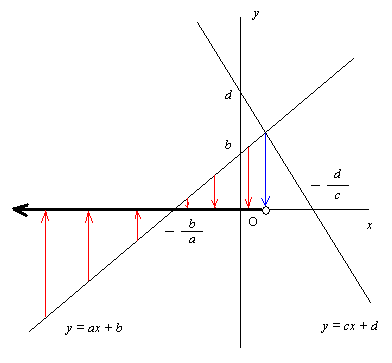
更に, f(x) = ax + b, g(x) = cx + d, a ≠ 0, c ≠ 0, a > c として f(x) < g(x) を考える。
普通に解くと ax + b < cx + d, (a - c)x < d - b で a > c だったから x < (d - b)/(a - c) となる。
ここで y = f(x) と y = g(x) の graph を描いてみると, f(x) < g(x) とは f(x) の graph が g(x) の graph より下にある部分の x 座標の範囲を求めていることになっている。