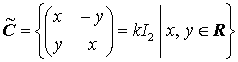を考える。 明らかに
であるから, C̃ に (M2(R)
の) 加法と乗法が考えられる。集合
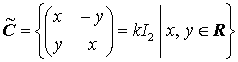を考える。 明らかに
であるから, C̃ に (M2(R)
の) 加法と乗法が考えられる。
| 0 = | ( | 0 | -0 | ) | , I2 = | ( | 1 | -0 | ) | , kI2 = | ( | k | -0 | ) | ∈ C̃ |
| 0 | 0 | 0 | 1 | 0 | k |
は明らかである。さて, 先ず C̃ が加法について可換群であることを示そう。
| ( | x1 | -y1 | ) | + | ( | x2 | -y2 | ) | = | ( | x1 + x2 | -(y1 + y2) | ) |
| y1 | x1 | y2 | x2 | y1 + y2 | x1 + x2 |
だから C̃ は加法について閉じており, 可換であることは M2(R) が可換であることから従う。 又 0 が要素であることから加法の単位元が存在することが分かる。 更に C ∈ C̃ の時 C + (-C) = (-C) + C = 0 であり, -C ∈ C̃ は明らかであるから, 逆元も存在する。 よって (C̃, +) は加法群である。
次に C̃* = C̃＼{0} が乗法群であることを示す。
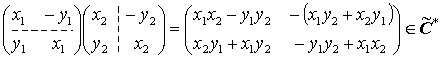
であるから乗法について閉じている。 I2 が要素であるから乗法の単位元が存在する。 逆元については
| det | ( | x1 | -y1 | ) | = x12 + y12 ≠ 0 |
| y1 | x1 |
であるから
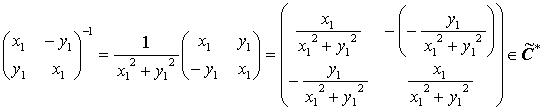
となって, 存在することが分かる。 よって (C̃*, ・) は乗法群である。
C̃ ⊂ M2(R) で M2(R) は環だから (C̃, +. ・) に関し分配法則が成り立ち, 従って C̃ は (M2(R) の部分) 環である。 よって C̃ は体である。
更に C̃ は可換体である。 というのも
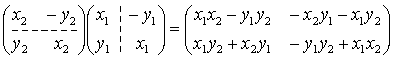
であって, これを上記のものと比較すれば可換であることが分かるからである。
さて
| J = | ( | 0 | -1 | ) |
| 1 | 0 |
と置くと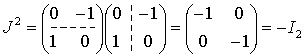 
である。 又 C̃ = RI2
Å RJ (直和) であることもすぐに分かる。 実際
| ( | x | -y | ) | = | ( | x | 0 | ) | + | ( | 0 | -y | ) | = xI2 + yJ |
| y | x | 0 | x | y | 0 |
だからである。
ここで R̃ → R という同型から, xI2 + yJ → x + iy 特に I2 → 1, J → i (小文字の I) という対応を考える。 これは一対一で, 上記から J2 = - I2 ⇔ i2 = -1 であるから, 写像 xI2 + yJ → x + iy による C̃ の像 C は C̃ と (体として) 同型になる。 この i を虚数単位 imaginary unit という。
又 xI2 + yJ への対応を見れば
という (vector としての)
同型も成り立つ。 但し, C̃
には積が入っているので R 2 の積は C̃
での行列の要素としては第一列で考えているとして良い。 この時 C∋ (x, y) と考えると, これは次のように図示できる。
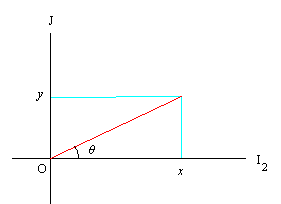
さて今, z ∈ C としよう。 この時, 上記の対応から ∃! x ∃! y ∈ R: z =
x + iy であるが,`z = x - iy ∈ C を考え, z の
(複素) 共役 (complex) conjugate という (以下`z の前に不要な
space があるが, これは Symbol font の所為であって, 普通は必要がないので注意してください)。 上記の図から |z| = √(z`z)
= √(x2 + y2) と定義し, z ∈ C の絶対値という。
明らかに |z| = |`z|. そして明らかに
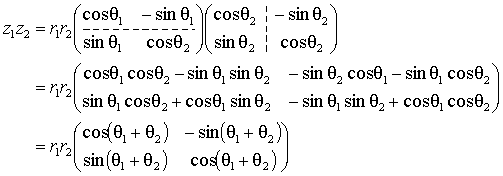, 一寸計算すれば,
も分かる。 そして z ≠ 0 の時
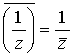であるが, 前に見たように 1/z =`z/(z`z)
= `z/|z|2 である。
ここまでで考えてきた C の元を複素数 complex number という。
上記の図で z = x + iy と考えるとき, ベクトル 0z が I2 軸と作る角 θ を z の偏角 argument といい θ = arg(z) と書く。 すぐ分かるように
z = |z|(cos arg(z) + i sin arg(z))
である。 これを複素数の極表示という。
今 θ = arg(z), r = |z| > 0 とし, 極表示を C̃ に引き戻して考えると
| z = | r | ( | cos θ | -sin θ | ) |
| sin θ | cos θ |
である。
| zk = | rk | ( | cos θk | -sin θk | ) | k = 1, 2 |
| sin θk | cos θk |
とすると
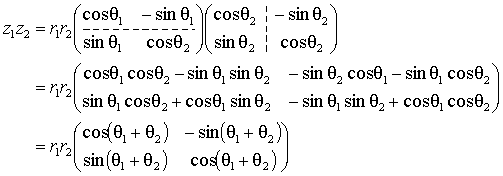
が加法公式からいえるが, 角度 θ1, θ2 の回転変換の合成であるから, これで一般角に関する加法公式の別証をしたことにもなっている。 このことから
|z1z2| = |z1||z2|, arg(z1z2) ≡ arg(z1) + arg(z2) (mod 2π)
が分かる。 このあとの方の式の意味は (左辺 - 右辺) ∈ 2πZ である。
今述べたことから直ちに de Moivre (ド・モアヴル) の公式
zn = (r(cos θ + i sin θ))n = rn(cos nθ + i sin nθ), for n ∈ Z
を得る。 従って
z1/n = r1/n(cos((θ + 2kπ)/n) + i sin((θ + 2kπ)/n)), for k = 0, 1, 2, ..., n
を得る。
よって特に, x に関する二次方程式 ax2 + bx + c = 0, a ≠ 0 は, a, b, c ∈ C で解を持つことが分かる。 実は一般の n 次方程式で解を持つことが分かるが, これを代数学の基本定理という。 この証明は難しいので他の代数学 (又は位相幾何学, 或いは解析学) の本にゆだねることにする。
今後 A = (ajk) に於いて, ajk ∈ C であるとして考えることもある。
さて, z = x + iy, x, y ∈ R とするとき`z = x - iy であったが, これらから
x = (z +`z)/2,
y = (z -`z)/(2i)
である。 この x, y を各々 z の実部 real part, 虚部 imaginary part といい, Âz = Re(z), Áz = Im(z) と書く。 即ち
Âz = Re(z) = (z +`z)/2,
Áz = Im(z) = (z -`z)/(2i)
(Â はドイツの文字 Frakutur の大文字の R, 同様に Á は I である)。