.題名に反して, 先ず, 対数函数の微分から。 定義に従って途中までやると
.
ここで対数法則を用いると
であるから, lim と loga は交換可能 --- つまり limh→0loga(1 + h/x)1/h = loga limh→0 (1 + h/x)1/h --- だということは, (本当は証明を要するが) グラフがつながっていることから明らかとしておくと, 問題は
である。 もう少し計算を進める為に, h/x = 1/t と置く。 このあとはかなり感覚的な話であるが, h → 0 となるとき, t → ±∞ なのだが, とりあえず t → +∞ としておく。 記号 ∞ は Wallis という人が考えた記号で, + でどんな数よりも大きい数のことである。 無限大 infinity を表す。 こうすると
となる。 1/x 乗はとりあえず置いておくと, 問題は 
なのであるが, さしあたって t
を自然数と仮定して調べてみると, これは 3
よりも小さい数に 1
から段々大きくなりながら近付いていくことが分かる。
実数の理論によって --- ここが難しい所なのだが ---
これはある一定の値に近付く (正確には収束する
converge) ことがいえて, それを記号で Leonhard Euler (オイラー)
にしたがって e と書く。 この e を 「自然対数の底」
又は Napier 数 という。 もう一度書くと
.
実際の値は (小数点以下約 2000 桁) e = 2.7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 2746639193 2003059921 8174135966 2904357290 0334295260 5956307381 3232862794 3490763233 8298807531 9525101901 1573834187 9307021540 8914993488 4167509244 7614606680 8226480016 8477411853 7423454424 3710753907 7744992069 5517027618 3860626133 1384583000 7520449338 2656029760 6737113200 7093287091 2744374704 7230696977 2093101416 9283681902 5515108657 4637721112 5238978442 5056953696 7707854499 6996794686 4454905987 9316368892 3009879312 7736178215 4249992295 7635148220 8269895193 6680331825 2886939849 6465105820 9392398294 8879332036 2509443117 3012381970 6841614039 7019837679 3206832823 7646480429 5311802328 7825098194 5581530175 6717361332 0698112509 9618188159 3041690351 5988885193 4580727386 6738589422 8792284998 9208680582 5749279610 4841984443 6346324496 8487560233 6248270419 7862320900 2160990235 3043699418 4914631409 3431738143 6405462531 5209618369 0888707016 7683964243 7814059271 4563549061 3031072085 1038375051 0115747704 1718986106 8739696552 1267154688 9570350354 0212340784 9819334321 0681701210 0562788023 5193033224 7450158539 0473041995 7777093503 6604169973 2972508868 7696640355 5707162268 4471625607 9882651787 1341951246 6520103059 2123667719 4325278675 3985589448 9697096409 7545918569 5638023637 0162112047 7427228364 8961342251 6445078182 4423529486 3637214174 0238893441 2479635743 7026375529 4448337998 0161254922 7850925778 2562092622 6483262779 3338656648 1627725164 0191059004 9164499828 9315056604 7258027786 3186415519 5653244258 6982946959 3080191529 8721172556 3475463964 4791014590 4090586298 4967912874 0687050489 5858671747 9854667757 5732056812 8845920541 3340539220 0011378630 0945560688 1667400169 8420558040 3363795376 4520304024 3225661352 7836951177 8838638744 3966253224 9850654995 8862342818 9970773327 6171783928 0349465014 3455889707 1942586398 7727547109 6295374152 1115136835 0627526023 2648472870 3920764310 0595841166 1205452970 3023647254 9296669381 1513732275 3645098889 0313602057 2481765851 1806303644 2812314965 5070475102 5446501172 7211555194 8668508003 6853228183 1521960037 3562527944 9515828418 8294787610 8526398139 5599
これは Visual BASIC で計算させたものであるが, 上記の定義の式から計算したものではない。 もっと効率の良い方法で計算してある。 又無理数で, 円周率 π と同様 「超越数」 と呼ばれる数である。 最初の数桁は 「鮒一箸二箸, 一箸二箸, 至極美味しい」 等と言って覚えるのが一般的なようである。 尚, ここに JAVA でこの数値を計算させる page がある。 (10000 桁出ている page もある)
さて, 話を元に戻して,
であるから,
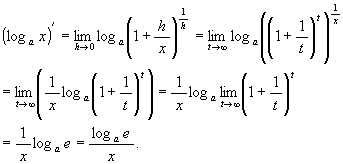
ここで普通 loge x のことを x に関する自然対数といい, 解析学 (微分積分学) では, 底 e を省略して書く。 そうすると, 微分が簡単になる。 又一般の底の時には, 底の変換公式を用いて次のようにするのが通例である。
,
.
さて, こうしておくと, 指数函数は, 対数函数の逆函数なので, 微分は次のようになる。
このように指数函数 y = ex は微分しても変化のない唯一の函数である。
一般の底では 
なので, 合成函数の微分を用いると
このように指数函数でも, 底が e であるほうが解析学にとっては面倒でなくて, 都合が良いのである。
log x は真数である為の条件として x > 0 という条件が課されているが, x < 0 のときに log(-x) は定義されて, 合成函数の微分によって (log(-x))' = -1/(-x) = 1/x となって微分は等しくなる。 そこで普通公式として, 絶対値の記号 | | を用いて
(log |x|)' = 1/x
という形で書かれることが多い。
但し, 解析函数 --- という非常に性質の良い函数 --- としての立場からすると, log (-x) = log (-1×x) = log (-1) + log x であり, --- log (-1) とは何かという問題をとりあえず無視すると --- log (-1) は定数であるから, 微分の結果 0 となるので, 定義域にこだわらず (log x)' = 1/x としておいて良いわけである。 尤もこの議論は解析函数論としては正しいが, 通常の教科書 (特に高校の教科書) に於いては, 扱われないので, log |x| の微分として覚えておくべきである。
補足：
10 を底とする対数 log10 x を常用対数と呼び, 我々が 10 進法を用いている関係上, この常用対数が応用方面では頻出する。 そういうわけで, 数学以外の分野では屡々この常用対数の方を底を省略する。 そういう場合, 自然対数の方を ln x と表記する。 私の持っているドイツ語の辞書には, 常用対数は gewönlicher Logarithmus というので lg x と表記すると書いてあるが, Knuth の本では 2 を底とする対数を lg x と表記している。 従って最も安全なのは, 自然対数を ln x と表記し, それ以外は全て底を書くことだが, この site では数学の常識に従って自然対数のみ, 底を省略して log x と表記する。
尚, 常用対数を logcom x, 自然対数を lognat x と書く流儀もある。
指数函数の微分が定義に従って出来ないという書き込みが合ったので一応書いておこう。
一般に f(x) = ax を微分する (a > 1)。 定義から
f'(x) = limh→0 (ax+h - ax)/h
= limh→0 (axah - ax)/h
= ax limh→0 (ah - 1)/h.
ここで先ず h > 0 とすると, ah > 1 だから ah = 1 + 1/t と置けて, h → 0 の時 t → +∞. 又置き方から h = loga (1 + 1/t). 従って
f'(x) = ax limt→∞ (1/t)/loga (1 + 1/t)
= ax limt→∞ 1/(t loga (1 + 1/t))
= ax limt→∞ 1/loga (1 + 1/t)t
= ax / loga e = ax log a.
h < 0 の時も同様にして s = -h と置くと
(ah - 1)/h = (a-s - 1)/(-s)
= -(1/as - 1)/s = (1 - 1/as)/s
= ((as - 1)/s)・(1/as)
であることを用いれば, 上記と同様になる。
0 < a < 1 の時も, ほぼ同様である (h < 0 の時に ah > 1 に注意すればよい)。
良く見てみると, これも殆ど逆函数の微分をなぞっているだけだと分かる。
2ch の数学板 ◆ わからない問題はここに書いてね ５０ ◆ スレッドに次のような書き込みがあった。
623 名前：１３２人目の素数さん ：02/09/14 21:02
文系学生です。 以下のページの「lim と log は交換可能だ」の意味がわかりません。
http://isweb23.infoseek.co.jp/school/phaos/diff2/explog.htm
どなたかお教え下さい。
624 名前：１３２人目の素数さん ：02/09/14 21:10
>>623
limを先に計算してもlogを先に計算しても計算結果が同じ
(これに対するお礼は省略)
というわけなのでそのことに関する補足を書いておいたが, 出来たらこういう質問は本人に直接して欲しい (^_^; 尚, ここも参照のこと。