その他の数列

「その他の数列」というとあまりにおおざっぱだが, 次の項目が書かれている。

1. 階差数列
2. S - rS 法
3. 第 n 部分和が与えられているもの。
4. その他
5. 二項定理

1. 階差数列

[定義]

数列 {a_n} に対し b_n = a_n+1 - a_n という数列を考え, この数列をもとの数列の (第一次) 階差数列 progression of differences という。 通常 {Δa_n} と書かれる。 (記号 Δ はギリシャ文字のデルタの大文字。)

同様に第二次階差数列 Δ²a_n = Δa_n+1 - Δa_n というのも考えられ, 以下同様に第 n 次階差数列 Δⁿa_n = Δ^n-1a_n+1 - Δ^n-1a_n というものが定義される。

もしも第一次階差数列 Δa_n が n の式で求まるならば, n > 1 の時,

a_n = a₁ + Σ_k=1^n-1Δa_k

注: Σの上端に注意。 n = 1 は別扱いであることに注意。

[証明]

a₁ + Σ_k=1^n-1Δa_k = a₁ + (a₂ - a₁) + (a₃ - a₂) + (a₄ - a₃) + … + (a_n - a_n-1) = a_n.

一応数学的帰納法でも証明しておく。

n = 2 の時 rhs = a₁ + Σ_k=1¹Δa_k = a₁ + Δa₁ = a₁ + (a₂ - a₁) = a₁ = lhs.

よって, a_n+1 = a₁ + Σ_k=1ⁿΔa_k を証明すればよいが
rhs = a₁ + Δa_n + Σ_k=1^n-1Δa_k = (a₁ + Σ_k=1^n-1Δa_k) + Δa_n
= a_n + (a_n+1 - a_n) = a_n+1 = lhs
で証明された。

例) 次の数列について, 一般項 a_n と第 n 部分和 S_n を推定せよ。

1, 2, 4, 7, 11, 16, ......

[解]

Δa₁ = 2 - 1 = 1
Δa₂ = 4 - 2 = 2,
Δa₃ = 7 - 4 = 3,
Δa₄ = 11 - 7 = 4,
Δa₅ = 16 - 11 = 5,
より, Δa_n = n と推定される。 よって n > 1 の時

a_n = 1 + Σ_k=1^n-1k = 1 + n(n - 1)/2 = (n² - n + 2)/2.

この式は n = 1 の場合をも含んでいる (という意味は, この式に n = 1 を代入すると a₁ = (1 - 1 + 2)/2 = 1 となって, もとの数列の初項と一致しているという意味である。 問題によってはこうならないときもあるので注意が必要である)。

S_n = Σ_k=1^n-1 (k² - k + 2)/2
= (1/2)・((n-1)n(2n -1)/6 + n(n - 1)/2 + 2(n - 1))
= (1/2)・((n - 1)/6)(n(2n -1) + 3n + 12)
((n - 1)/12)(2n² + 2n + 12)
(n - 1)(n² + n + 6)/6.

注: ここで求めた一般項は実は補間公式で求めたものと同じである。

実は上の例において Δa₁ = 1, Δ²a₁ = 1, Δⁿa₁ = 0, n > 2 が分かるので,

a_n = a₁ + Δa₁(n - 1) + Δ²a₁(n - 1)(n - 2)/2
= 1 + (n - 1) + (n - 1)(n - 2)/2
= (2 + 2(n - 1) + (n - 1)(n - 2))/2
= (2 + 2n - 2 + n² - 3n + 2)/2 = (n² - n + 2)/2.

というように, Newton の補間公式から簡単に求まる。

このように, 実は階差数列からもとの数列を復元する方法は Newton の補間公式をなぞっているのに過ぎず,

a_n = a₁ + Δa₁(n - 1) + Δ²a₁(n - 1)(n - 2)/2 + … + Δ^ka₁(n - 1)(n - 2)…(n - k)/(k!)

となる (但し {Δ^k+1a_n} = {0} の場合。 勿論, 階差数列はいつか {0} になるとは限らないので, Newton の補間公式だけから全てが求まるわけではない)。 ここで階乗 ! についてはここを参照のこと。再掲すると 0! = 1, 自然数 m に関し, m! = (m-1)!×m = m(m-1)(m-2)…2×1.

2. S - rS 法

これは 「等比数列とその和」 のところで一寸述べたものであるが, 一般的には述べ難いので, 例を一つ挙げて, 方法論を分かってもらうことにする。

例) S_n = 1・2 + 2・2² + 3・2³ + … + n・2ⁿ を計算して簡単にせよ。

[考察]

これは, (等差数列)×(等比数列) という形をした数列の第 n 部分和であると考えられる。 そこで, 等比数列の部分の公比 2 を掛けて, これから引いてみるということをする。 やってみると上手くいくことが分かる。

[解]

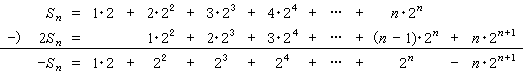
でこの右辺の (初項が含まれているのは単なる偶然であるが) 初項から第 n 項までは, 初項 2, 公比 2 の等比数列であるから, 公式によって

-S_n = 2(2ⁿ - 1)/(2 - 1) - n・2ⁿ⁺¹
= 2ⁿ⁺¹ - 2 - n・2ⁿ⁺¹
= -(n - 1)・2ⁿ⁺¹ - 2.

よって S_n = (n - 1)・2ⁿ⁺¹ + 2.

3. 第 n 部分和が与えられているもの。

これは既に 「等差数列とその和」 のところで述べたものである。

第 n 部分和 Sn が与えられているとき

a₁ = S₁,
a_n = S_n - S_n-1, n > 1.

勿論これは, S_n = Σ_k=1ⁿa_k だから, Σ の定義 Σ_k=1ⁿa_k = a_n + Σ_k=1^n-1a_k, n > 1 を書き換えたものに過ぎない。

例を二つばかりあげよう。

(1) 第 n 部分和が S_n = n² の時, もとの数列の一般項 a_n を求めよ。

[解]

a₁ = S₁ = 1² = 1.

n > 1 の時
a_n = S_n - S_n-1 = n² - (n - 1)² =(n + (n - 1))(n - (n - 1)) = 2n - 1.

この式は n = 1 の場合をも含んでいる。

(2) 第 n 部分和が S_n = 2ⁿ の時, もとの数列の一般項 a_n を求めよ。

[解]

a₁ = S₁ = 2¹ = 2.

n > 1 の時
a_n = S_n - S_n-1 = 2ⁿ - 2^n-1 = 2・2^n-1 - 2^n-1 = (2 - 1)2^n-1 = 2^n-1.

(こちらの場合は, n = 1 の場合を含んでいない。 解答を書く時は, 場合分けして列記するしかない)

4. 一般項が和の形をしているもの。

(1) 数列, 9, 99, 999, 9999, ...... の一般項 a_n 及び第 n 部分和 S_n を求めよ。

[解] a_n = 10ⁿ - 1 と推定される。

S_n = Σ_{k = 1} ⁿ a_k = Σ_{k = 1} ⁿ (10^k - 1) = Σ_{k = 1} ⁿ 10^k - Σ_{k = 1} ⁿ 1
= 10(10ⁿ - 1)/(10 - 1) - n = 10(10ⁿ - 1)/9 - 9n/9
=(10^{n+ 1} -9n - 10)/9.

(2) 数列 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4, ...... の一般項 a_n 及び第 n 部分和 S_n を求めよ。

[解] a_n = 1 + 2 + 3 + … + n = Σ_{k = 1} ⁿ k = n(n + 1)/2.
∴S_n = Σ_{k = 1} ⁿ(k(k + 1)/2) = (1/2)Σ_{k = 1} ⁿ(k(k + 1))
= (1/2)(n(n + 1)(n + 2)/3) … 和の記号 Σ とその公式の例 (1)
= n(n + 1)(n + 2)/6.

5. 二項定理

一寸関係ないが, ついでだから, ここで二項定理 binomial theorem を紹介しておく。

先ず上記にも述べたが, n ≧ 0, n ∈ Z に関して

0! = 1,
n! = (n-1)!×n = n(n-1)(n-2)…2×1

を n の階乗 factorial という。

_nC_r = n!/(r!(n - r)!), n, r ∈ Z, n ≧ 0, 0 ≦ r ≦ n を二項係数 binomial coefficient という。

二項係数の性質:

1. _nC₀ = _nC_n = 1.
2. _nC_r = _nC_n-r.
3. _n+1C_r+1 = _nC_r + _nC_r+1, 0 ≦ r ≦ n - 1.

[証明] rhs = right hand side, lhs = left hand side.

1. _nC_n = n!/(n!(n - n)!) = n!/(n!・0!) (= _nC₀) = 1.

2. rhs = n!/((n - r)!(n - (n - r))!) = n!/((n - r)!(n - n + r)!) = n!/((n - r)!r!) = lhs.

3. rhs = n!/(r!(n - r)!) + n!/((r + 1)!(n - (r + 1))!)
= (r + 1)・n!/((r + 1)!(n - r)!) + (n - r)・n!/((r + 1)!(n - r)!)
= ((r + 1) + (n - r))・n!/((r + 1)!(n - r)!)
= (n + 1)!/((r + 1)!((n + 1) - (r + 1))!) = lhs.

この三番目の性質を用いて, 次の二項定理が証明される。

[定理]

n∈ Z, n ≧ 0 に対し, 次式が成立する。

(x + y)ⁿ = Σ_r=0ⁿ_nC_rx^n-ry^r.

[証明] 数学的帰納法による。

n = 0 の時は両辺とも 1 となって成立している。

(x + y)ⁿ⁺¹ = (x + y)ⁿ・(x + y) … 冪乗の定義
= Σ_r=0ⁿ_nC_rx^n-ry^r(x + y) … 帰納法の仮定
= Σ_r=0ⁿ_nC_rx^n-ry^r・x + Σ_r=0ⁿ_nC_rx^n-ry^r・y … 分配法則
= Σ_r=0ⁿ_nC_rx^n-r+1y^r + Σ_r=0ⁿ_nC_rx^n-ry^r+1 … 指数法則
= Σ_r=0ⁿ_nC_rx^n+1-ry^r + Σ_r=0ⁿ_nC_rx^(n+1)-(r+1)y^r+1.

さてここで, 後ろの方だけ, k = r + 1 と置き換えると

lhs = Σ_r=0ⁿ_nC_rx^n+1-ry^r + Σ_k=1ⁿ⁺¹_nC_k-1x^(n+1)-ky^k.
= _nC₀x^n+1-0y⁰ + Σ_r=1ⁿ_nC_rx^n+1-ry^r + Σ_k=1ⁿ_nC_k-1x^n+1-ky^k + _nC_nx^(n+1)-(n+1)yⁿ⁺¹
= xⁿ⁺¹ + Σ_r=1ⁿ_nC_rx^n+1-ry^r + Σ_k=1ⁿ_nC_k-1x^(n+1)-ky^k + yⁿ⁺¹
= xⁿ⁺¹ + Σ_r=1ⁿ(_nC_r + _nC_r-1)x^n+1-ry^r + yⁿ⁺¹ … 分配法則

第二項で i = r - 1 と置くと

lhs = xⁿ⁺¹ + Σ_i=0^n-1(_nC_i+1 + _nC_i)x^n+1-(i+1)yⁱ⁺¹ + yⁿ⁺¹
= xⁿ⁺¹ + Σ_i=0^n-1_n+1C_i+1x^n+1-(i+1)yⁱ⁺¹ + yⁿ⁺¹ … 上記の公式 3.
= _n+1C₀x^n+1-0y⁰ + Σ_i=0^n-1_n+1C_i+1x^n+1-(i+1)yⁱ⁺¹ + _n+1C_n+1x^(n+1)-(n+1)yⁿ⁺¹

ここで再び r = j + 1 と置くと

lhs =  _n+1C₀x^n+1-0y⁰ + Σ_r=1ⁿ_n+1C_rx^n+1-ry^r + _n+1C_n+1x^(n+1)-(n+1)yⁿ⁺¹
= Σ_r=0ⁿ⁺¹_n+1C_rx^n+1-ry^r = rhs.

次へ
数列とその極限の目次へ